Just like sets are in bijection with functors \(\mathbf{1}\rightarrow\mathbf{Set}\), we can also associate natural transformations
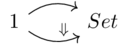
with functions.
In the language of functor categories, this claim is to say \(\mathbf{Set}^1\) is equivalent to \(Set\).